QC検定を取得したけど何の役に立つんだろう?
今回は品質管理検定(QC検定)を転職に活かす方法を説明します。
結論は「現職場で統計的品質管理を実践すること」です。
このような記事を書くのは次の理由。
他の人のブログなどを見ていると「QC検定に最短で合格する方法!」とか結構ありがち。
それ自体はいいんですが、
取得した人がQC検定を取ることをゴールとしてしまっているのではないかと感じたから。
もちろん頑張って勉強して検定を取得した事は大事です。
しかし、転職活動で人事の方にアピールするためには
QC検定で学んだ知識をどのように活用し、転職先の品質管理へどのように貢献できるか
を語らないと意味がありません。
語るためにはどうしても「現職場で統計的品質管理を実践した経験」が必要になってくる という理屈です。
今回は「そう言われてもどうやって活用したらいいかわからないよ!」というあなたに
活用しやすいモデルケースを3つ挙げて解説していきたいと思います。
本記事を読むことでQC検定を転職に活かすための具体的方法がわかり、転職成功に近づきます。
活用例1:工程能力指数による品質管理

QC検定レベル:2級~3級
このケースは工場の生産ラインなどで品質不良が出た際に、品質改善をする場合を想定しています
まずは現状把握のために製品のサンプルをランダムに抜き取ります
抜き取るサンプル数は30~50個を目安としてください
次に抜き取ったサンプルの特性値を測定しデータを集め、そのデータを可視化するため「ヒストグラム」を作成します
エクセルでヒストグラムを描くのは大変なので、こちらの記事を参考に統計解析ソフト「スタットワークス無料体験版」を使って描きます
ヒストグラムを作るのってめんどくさい。簡単に作れる方法はないの? 統計解析ソフトを使った「ヒストグラムの簡単な作り方」をご紹介します! […]
するとこのようにヒストグラムが書けるかと思います
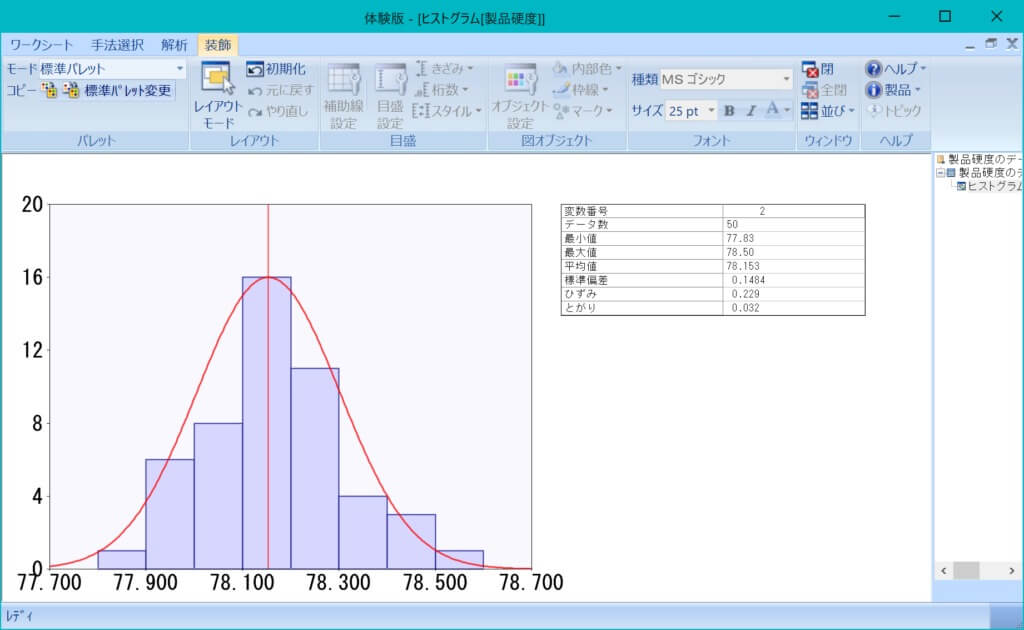
次に規格値を入力して「工程能力指数」を求めます
工程能力指数の求め方はこちらを参考にしてください
工程能力指数を簡単に計算する方法はないの?cp,cpkを素早く求めたい。 工程能力指数cp・cpkは”統計解析ソフト”で簡単に求められますよ。私はQC検定1級で、普段[…]
工程能力指数の判断は以下の指標を参考にします
1.67 > Cp (Cpk) ≧ 1.33 工程能力は十分である
1.33 > Cp (Cpk) ≧ 1.00 工程能力は十分とは言えないがまずまず
1.00 > Cp (Cpk) ≧ 0.67 工程能力は不足している
0.67 > Cp (Cpk) 工程能力は非常に不足している
おそらく今回は不良品が発生しているためCp、Cpkのどちらか(もしくは両方)が1.00未満だと思います。
あなたはヒストグラムの形、平均値のかたより、バラつきの大きさから、平均値を規格の中央に合わせる のか ばらつきを低減するのか、もしくはその両方を考えて改善を行います。
改善の効果を検証するために改善後の生産ラインから同じようにサンプルを抜き取り工程能力指数で、その良し悪しを判断します
「母集団の特性の分布を推測し規格を満足することができるか」
という、統計的品質管理の基本と言える考え方を実践するモデルケースです
活用例2:2つの母集団の差を「検定」で判断する

QC検定レベル:1級~2級
このケースは製品に使用する材料はA材とB材のどちらが強度が高いか など2つの母集団を比較して判断する場合を想定しています
従来の材料選定方法はA材、B材での製品サンプルを各25個準備して、その強度の平均値だけを比較してたとすると、これはばらつきを考慮していないため非常に危険です
母集団を推定し、統計的な判断を行うための方法が「検定」です。
QC検定では検定統計量を暗記して乗り切った人もいるかもしれませんが
母集団の分布を想定し判断する「検定」は実務でこそ使うべき手法です
データは従来通り各25個程度集めれば十分です
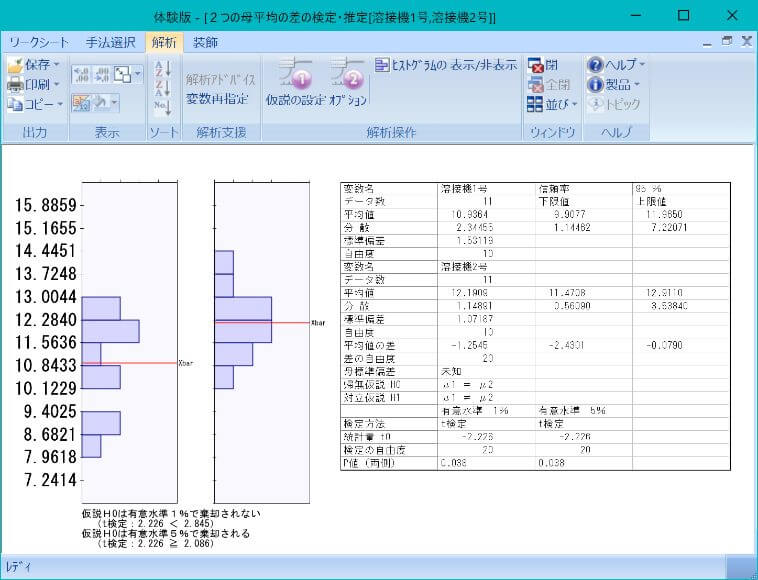
平均値に差があるかを判断する場合は「2つの母平均の差の検定」でt検定を行います
ばらつきに差があるかを判断する場合は「2つの母分散の比の検定」でF検定を行います
スタットワークス無料体験版を使えば簡単にできるのですが、まだ記事を準備していないので手計算で行います (今後作成していきます、すみません)
- 帰無仮説の設定
- 棄却域の設定
- 検定統計量の計算
- 判定
という流れで計算し、結論を導きます(計算方法はQC検定のテキストを参照ください)
「検定」を使って統計的に判断が下せる人材であるとアピールできるモデルケースです。
活用例3:実験計画法で設備の最適条件出し

QC検定レベル:1級~2級
このケースは生産技術者として設備の最適条件を「実験計画法」で求める場合を想定しています
まずは設備で設定できる「因子」と測定する「特性値」を決めます
因子の数と交互作用の有無により「一元配置」「二元配置」「多元配置」「直交表実験」となりますが、ここでは「二元配置」と仮定します。
因子が決まったら次に「水準」を決めます。
因子と水準が決まったら「二元配置実験(=全組み合わせ実験)」を行い、特性値を測定します。
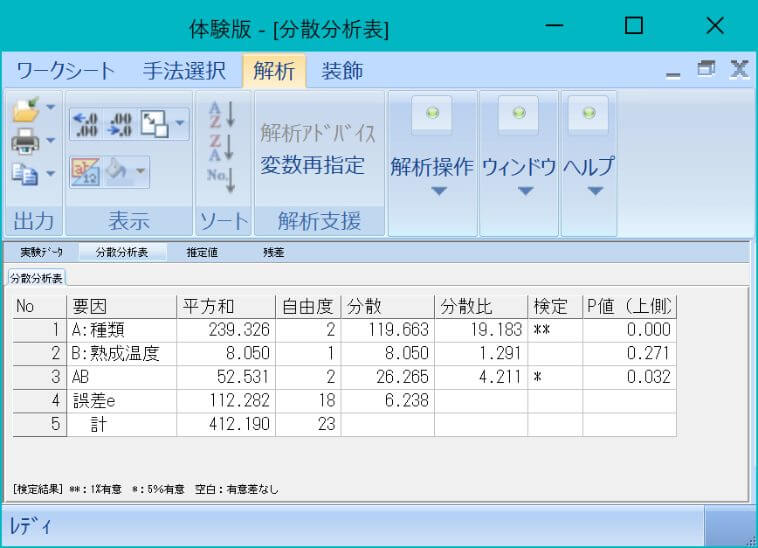
データがそろったら「分散分析表」を作ります。
これもスタットワークス無料体験版で簡単に計算できるのですが、まだ記事を作成していないので手計算で計算します (今後作成します、すみません)
分散分析表から統計的に有意と言える因子を見つけます
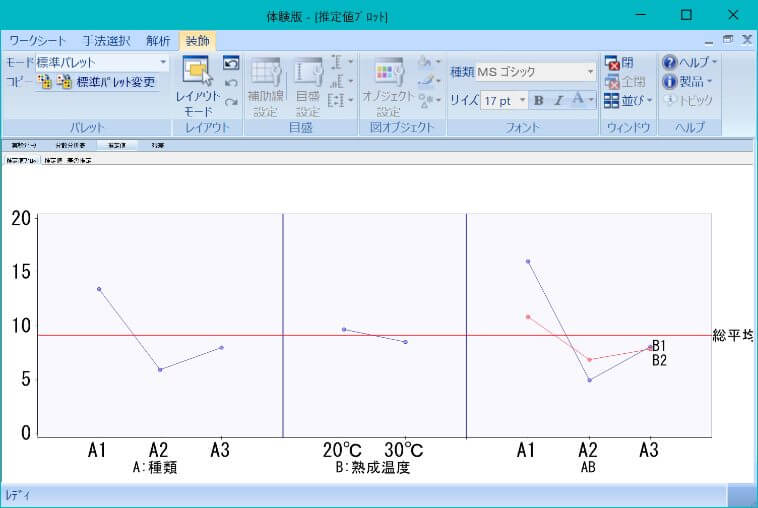
次に要因効果図から交互作用も考慮して最適な条件を選定します
実験計画法を活用して「統計的な分析をもとに設備条件を設定できる人材」とアピールできるモデルケースです。
転職にQC検定を活かす まとめ

今回は 既にQC検定に合格されたあなたが品質管理検定(QC検定)を転職に活かす方法を書いてきました
重要なのは 「QC検定で学んだ知識をどのように活用し、転職先の品質管理へどのように貢献できるか」をアピールできることです。
そのためにはモデルケースを参考に 現職場で1つでも統計的な品質管理を実践してみてください。
転職でQC検定を活かすには「QC検定の優遇案件が多い転職サイトを利用する」事も重要です。
こちらの記事もぜひ確認して下さいね。
自分に有利な転職サイトを探している人↓QC検定が優遇される転職サイトは?何件くらい需要があるのかな?何級の需要が多いか知りたいな。具体的にどんな求人があるの?こんな疑問を解[…]
もし、現時点でのご自身の「市場価値」が気になるというあなたは
こちらの「ミイダス」で筆者が実体験していますので、試してみるのもよいかと思います
ミイダスって実際どうなの?自分の市場価値ってどれくらいなんだろう?こんな悩みを解決します。 自分の市場価値を知っておくことはとても重要。でも世間と価値を比較するの[…]







