トライ(実験)を計画しているエンジニア
↓
効率の良いトライ方法を知りたいな。
記事の内容
- やってはいけないトライ(実験)方法
- 効率の良いトライ(実験)方法
私は製造業のエンジニアで、QC検定1級を活かしてQC検定講師やデータ解析を本業としています。
以前は生産技術者として、工場に生産ラインの導入などを行っていました。
※☞プロフィール詳細はこちら
統計手法を知らなかった頃は、今思うと随分無駄なトライを行ってきました。
上司や他部署も知識が無かったので、それが日常化。
あなたも試作品の評価や、設備の条件出しでトライを計画しているのでしょう。
しかし闇雲にトライを行っても効率が悪く、最悪の場合は判断を誤る事もあります。
結論:実験計画法を実践しよう。
今回はエンジニアがやってはいけないトライ方法を具体的にご紹介。
その上で、誰でも実践できる簡単な”実験計画法”のやり方を説明します。
本記事を読むと、効率の良いトライ方法が分かり、無駄な残業を減らして自分の時間を増やす事ができます。
やってはいけないトライ方法

- 勘と経験によるトライ
- 総当たりトライ
- 2因子間のマトリクス式トライ
- 他を固定して一元配置トライ
勘と経験によるトライ
一番、まずいトライはこちら。
勘と経験で因子の水準を変えていくトライ。
例えばこんな感じ。
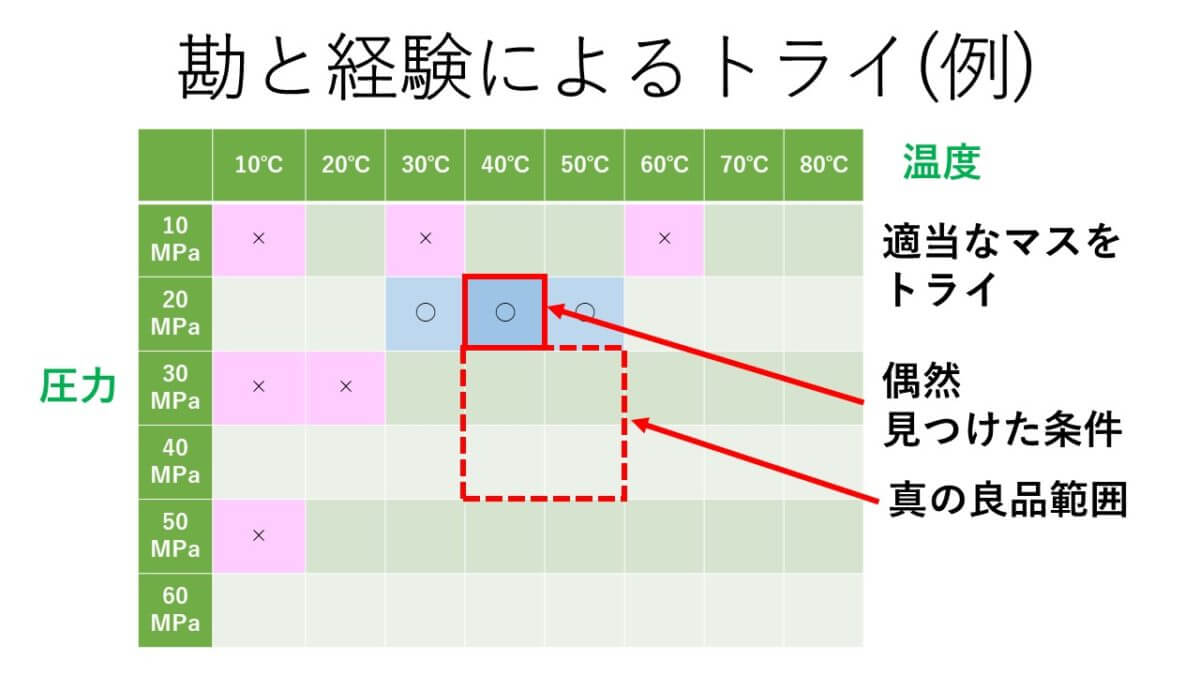
これは極端ですが、時間に追われていると、こんなトライもやってしまう。
職務経験が長いベテランさんがいる職場でありがち。
実際に私も先輩たちがやっているのも見ましたし、自分でもやっていました。
ばらつきに耐えられませんし、穴だらけなので今すぐにやめましょう。
総当たりトライ
全ての因子と水準の組み合わせを行うトライ
確かに最適な水準組み合わせを必ず見つけることが出来ます。
しかし、特性値に影響する因子と水準が増えるほど実験回数が膨大に。
結局全部やりきれないのが”あるある”。
統計手法なら、その何分の1のトライ回数で同じゴールにたどり着けます。
無駄な労力は無くしましょう。
2因子間のマトリクス式トライ
特性値に影響する2因子に限定して、マトリクスを作り、埋めていくトライ。
図にするとこんな感じ。
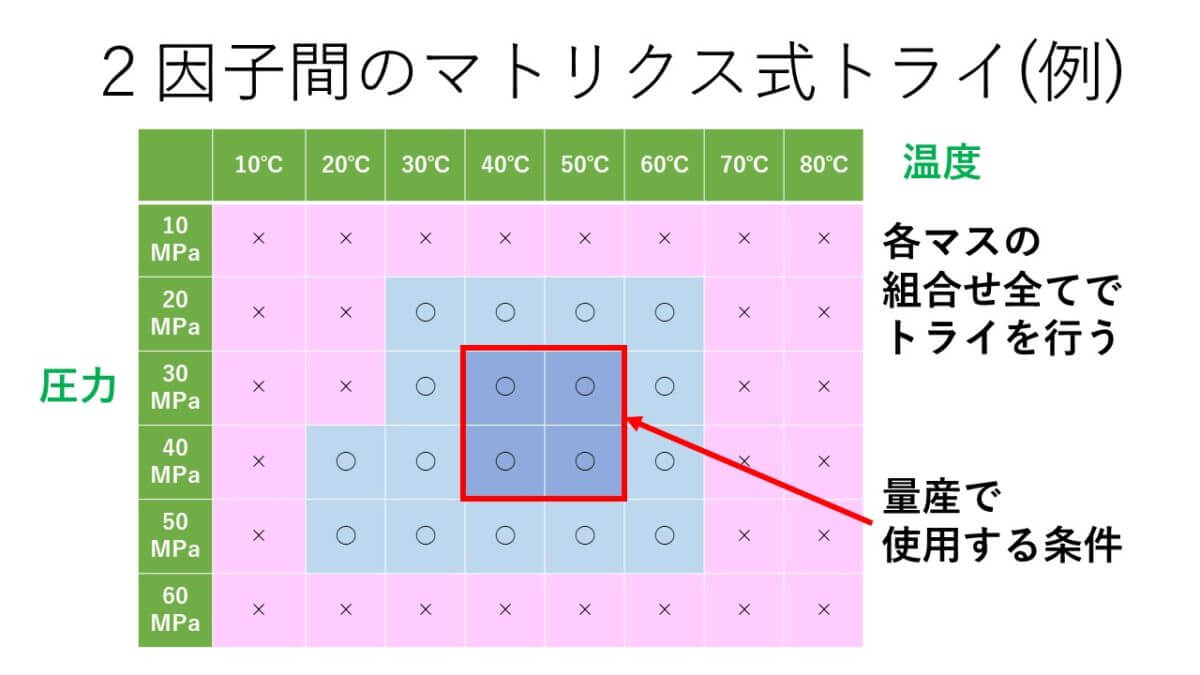
二次元のマトリクスで表せるから、資料にも載せやすい。
良品条件範囲を見つけたと安心感を得たい時にやりがち。
これの問題点は
- 水準数が増えるのでトライ回数がもの凄く多い
- 特性値に影響しているのは2因子とは限らない
- 繰り返しによるばらつきを見れない
特性値に影響している因子が本当に2因子だけなら有効な方法です。
しかし、実際は3因子以上の場合がほとんど。
それを無理やり2因子にまとめていませんか?
とにかくムダが多いし、穴もある。
”網羅的に調査できている”という錯覚に陥りやすい分、とても危険。
実験計画法によるトライなら3因子以上の組合せで計画可能。実験回数は半数以下。
全ての因子間の組み合わせで良品範囲が調べられます。
他を固定して一元配置トライ
標準条件を設定して、各因子を順番に一元配置トライを行う方法。
例えばこんな感じ。
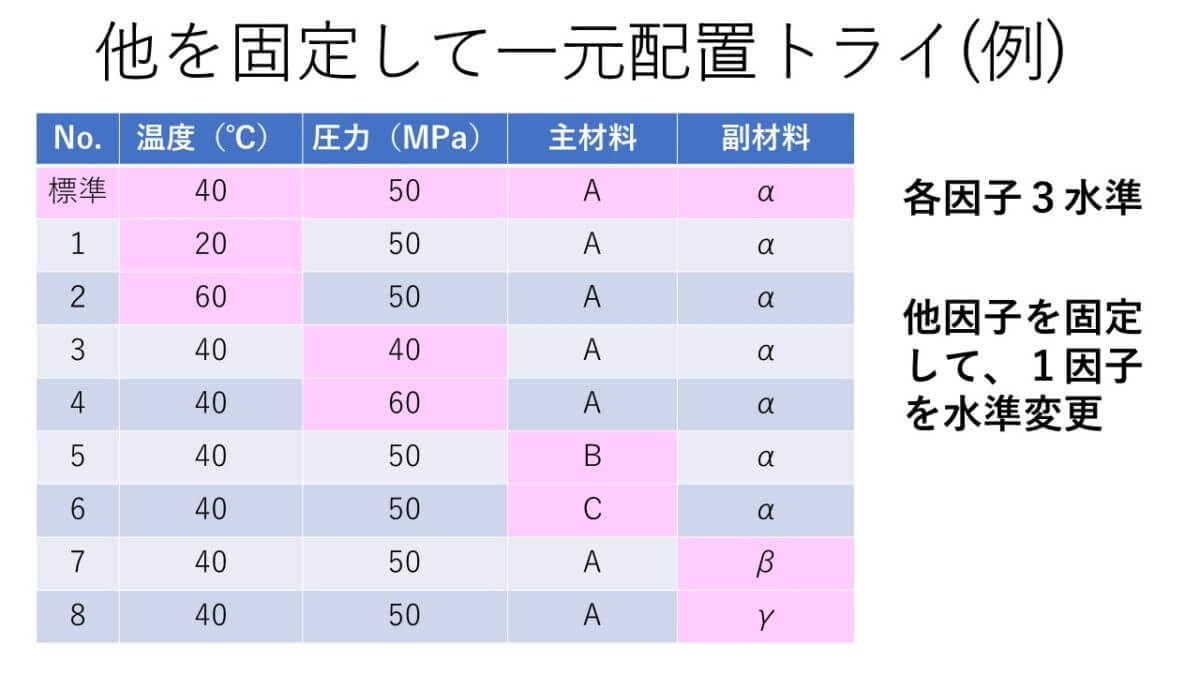
これもよくやられそうだけど、穴だらけ。
交互作用は全く見れていない。
なんとなく全ての組み合わせが確認出来ている”錯覚”に陥りやすいトライ。
実験計画法なら、全ての因子間の交互作用も確認できます。
効率の良いトライ方法

それをまとめたのがこちら。
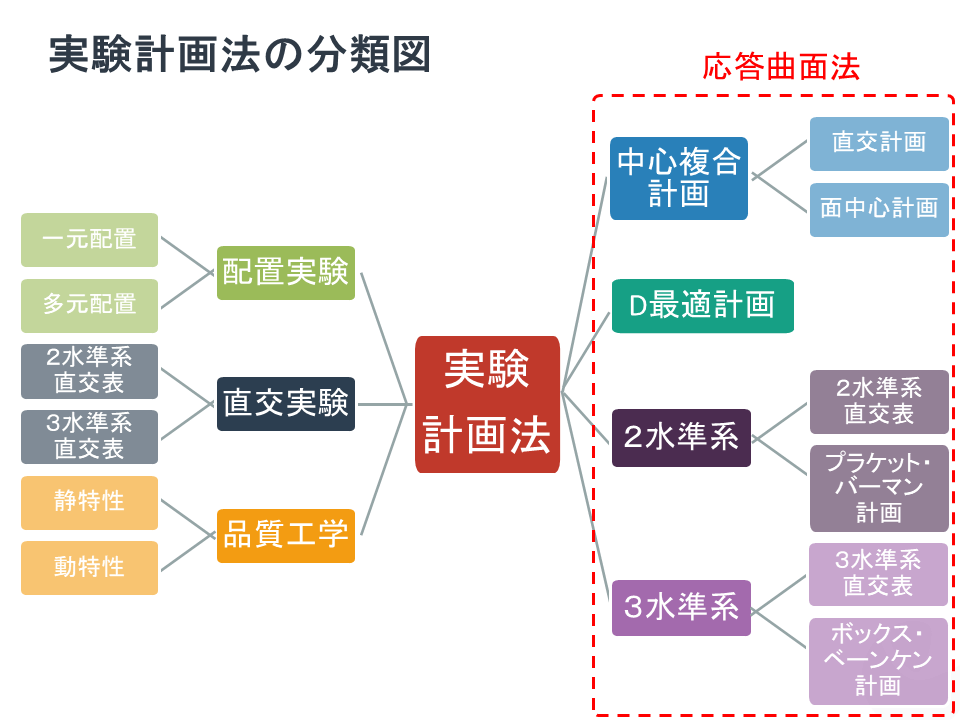
おすすめの計画
- 中心複合計画(直交)
- D最適計画
- プラケットバーマン計画
おすすめしない計画
- 配置実験
- 直交実験
おすすめ①:中心複合計画(直交)
| 実験回数の少なさ | 4.5 |
| 要因効果の推定精度(直交性) | 5.0 |
| 容易度 | 4.0 |
| 業務での使いやすさ | 3.0 |
| 総合 | 4.0 |
応答曲面法の1つ。
- 実験回数が少ない
- 因子間の効果が直交で推定精度が高い
- 割り付けがなく簡単
- 最適条件の探索向け
- 質的変数が扱えない
- 必要範囲外の水準での実験が必要
という特徴の計画法。
こちら「実験計画法のやり方!中心複合計画で実験回数を大幅に削減【簡単】」で詳しく解説しています。
おすすめ②:D最適計画
| 実験回数の少なさ | 4.5 |
| 要因効果の推定精度(直交性) | 4.0 |
| 容易度 | 4.0 |
| 業務での使いやすさ | 5.0 |
| 総合 | 4.5 |
応答曲面法の1つ。
- 実験回数が少ない
- 因子間の効果がわずかに交絡
- 割り付けがなく簡単
- 最適条件の探索向け
- 質的変数が扱える
- 必要範囲外の水準での実験が不要
質的変数・量的変数が扱えて、難しい割り付けが不要。
最も実務向けの万能な計画です。
実はD最適計画は欧米では主流の計画法。
彼らは効率の良い方法を追求。日本人はいつまでも手計算時代の直交表実験を教えています。
あなたはどちらを選びますか?
こちらの記事で、どの専門書にも載っていない具体的な実践方法を解説しています。
☞【劇的】QC検定1級の私が「実験回数を激減させる統計手法」を解説する
おすすめ③:プラケットバーマン計画
| 実験回数の少なさ | 4.5 |
| 要因効果の推定精度(直交性) | 5.0 |
| 容易度 | 3.0 |
| 業務での使いやすさ | 2.0 |
| 総合 | 3.5 |
応答曲面法の1つ。
- 実験回数が少ない
- 主効果の効果が直交で推定精度が高い
- 割り付けがなく簡単
- 因子のスクリーニング向け
- 最適条件の探索は出来ない
2水準で、特性に効いている因子を絞りこむ(スクリーニング)の為の計画。
最適条件の探索には使えないが、少ない実験で効いている因子を見つけられる。
用途は限定されますが、役立つ時はもの凄く役に立つ”卵焼き用のフライパン”みたいな計画。
こちらの「実験計画法のやり方!プラケット-バーマン計画で影響因子を絞り込む。」で詳しく解説していますよ。
おすすめしない①:配置実験
| 実験回数の少なさ | 1.0 |
| 要因効果の推定精度(直交性) | 5.0 |
| 容易度 | 5.0 |
| 業務での使いやすさ | 1.0 |
| 総合 | 3.0 |
総当たり実験。
- 実験回数が多い
- 全ての因子効果が分かる
- 何も考えなくてよいので簡単
- 因子・水準が増えると実施できない
お金と時間があるなら、確実な配置実験ですが、効率は最悪。
業務で使うのはおすすめしません。
おすすめしない②:直交実験
| 実験回数の少なさ | 3.5 |
| 要因効果の推定精度(直交性) | 5.0 |
| 容易度 | 1.0 |
| 業務での使いやすさ | 1.0 |
| 総合 | 2.5 |
直交表を使う実験を”直交実験”と言います。
その特徴。
- 直交表にうまくあてはまれば実験回数は少ない。
- 指定した因子の効果は推定できる
- 交互作用の有無を把握しているのが前提
- 割り付けが難しい
- 質的因子しか扱えない
日本でいまだに実験計画法の主流で教えられる”直交実験”ですが、実務では扱いづらい。
割り付けが分からず実験計画法を挫折する人はたくさんいます。
直交表は手計算の時代に考えられた方法。
コンピューターが使える時代にわざわざ直交表を使う必要はありません。
あなたは効率の良い実験を行いましょう。
直交表が使えない詳しい理由は「実験計画法=直交表はもう古い。今すぐやめるべき5つの理由【確信】」にて解説しています。
エンジニアがやってはいけないトライ方法 まとめ

今回はエンジニアがやってはいけないトライ方法を紹介しました。
具体的にはこの4つ。
- 勘と経験によるトライ
- 総当たりトライ
- 2因子間のマトリクス式トライ
- 他を固定して一元配置トライ
逆におすすめの実験計画法はこの3つ。
以下の記事で具体的な実践方法を解説しています。
- 応答曲面法の基本 中心複合計画(直交)
>>実験計画法のやり方!中心複合計画で実験回数を大幅に削減【簡単】 - 実務で使いやすい万能な計画 D最適計画
>>【劇的】QC検定1級の私が「実験回数を激減させる統計手法」を解説する - 因子の絞り込みに役立つ計画 プラケットバーマン計画
>>実験計画法のやり方!プラケット-バーマン計画で影響因子を絞り込む。
個別でアドバイスします(2021年4月10日更新)
読者の方から「自業務に対し個別でアドバイスがほしい」とのご要望をいただきました。
”ココナラ”というスキルマーケット※でお引き受けしています。
実務の実情に合わせた実験計画立てのアドバイス。及び、解析結果の考察まですべてサポート致します。ぜひご検討ください。
(※機密保持契約あり。企業名での領収書発行可)
こんな人におすすめ
- とにかく早く課題を解決したい!
- 実践しようとしたけど上手くいかない。
- 基礎からしっかり教えてほしい。
おすすめではない人
- プロジェクト納期に余裕がある。
- 独学で学びたい。
統計手法を習得するには、早く実践して”成功体験を得る”事が最も大切です。
この機会に実践して仕事を楽にしましょう(^^)
ご利用いただいた方の声(2021年12月11日更新)

購入して、とても満足しています。
サービス内容にも記載されていた通り、値段以上の価値がある経験ができました。チャレンジしてみたいと思っても、書籍やネットの情報では中々理解できず踏み切れなかったところ、分からないことを丁寧に分かりやすく説明して頂けるので、とても助かりました。
私のように実務で統計手法を試してみたいけど、難しそうで挑戦できていないという方や、少しでも実験を効率化して製品開発を行いたいという方は、書籍を買って独学でするよりも一度出品者様にご相談した方がより早く、理解を深めながら挑戦し、その効果を実感できると思います(もちろん相談後は書籍等で自分でも勉強してみるつもりですが)。
わからないことがあるたびに打ち合わせをお願いしても快く丁寧に対応してくださり、本当に感謝しています。
ココナラでこの方に巡り合えてご相談できて本当によかったと思っています。ありがとうございました。

書籍で手法の概要は理解できたものの、実際に自分で統計ソフトを用いてどのように作業を進めていけば良いのかがわからずに困っていたため、私の希望で立案から解析までをワークショップのような形式でサポートをお願いしました。
とても丁寧に対応していただき、理解を深めることができました。
今後もぜひ、お付き合いさせていただきたいと思いました。
ありがとうございました。
どちらのお客様も私のサポートを受けながら、ご自身の手で課題を解決されました。
このような高評価をいただけてとても光栄です。








